Writing an emulator: sound is complicated

2020-05-13 / Development, Emulator

That’s something I’ll be repeating a lot throughout this article, and probably a couple others, because, well, sound is complicated.

Wait, sorry, let me just get this out of my system:

Sound is complicated

At the time of this writing, my actual emulator still has no sound support. It’s partly due to the fact its development has been pretty much on hiatus for the whole time I’ve been busy writing these articles, but I also kept putting off sound implementation all along because, well… no, really, sound is hard.

Granted, there are easier ways to write a program that produces sound than coming up with an emulator, but even then sound feels noticeably more complex than any other thing I’ve had to do with code. Back when we were working with pixels, though displaying them took a bit of work, defining them was relatively straightforward: a small bunch of numbers defined a colored dot. A slightly larger bunch of those dots represented a frame at a point in time, and we only needed to tell SDL: “put those colored dots on screen now please”.

What is sound, even?

Note: I’m focusing on low-level signals in this article as this is the way we’ll have to implement sound in the emulator. This is by no means a guide to sound in SDL. Most of the examples I’ve seen online are way higher-level and easier to use, rely on WAV or OGG sound files, and unfortunately don’t really fit in with the way the Game Boy works internally.

I initially found sound harder to define. You can’t really just say “hey SDL, play a B flat tone now please”¹. What defines that B flat? If we gloss over a lot of complexity, sources say we can think of it as a frequency: approximately 466.164 Hz.

But that doesn’t tell us much about how that frequency should look like to a computer or SDL. With our pixel, the RGBA value was somewhat enough. Here, we only know that the sound we want to produce involves something that varies approximately 466.164 times per second. But what does that something even look like?

A periodic signal is often represented as a sinusoid. In our example, the sinusoidal signal would go through 466.164 oscillations (which I’ll indifferently refer to as “variations”, “periods” or “cycles” throughout the rest of this article) per second.

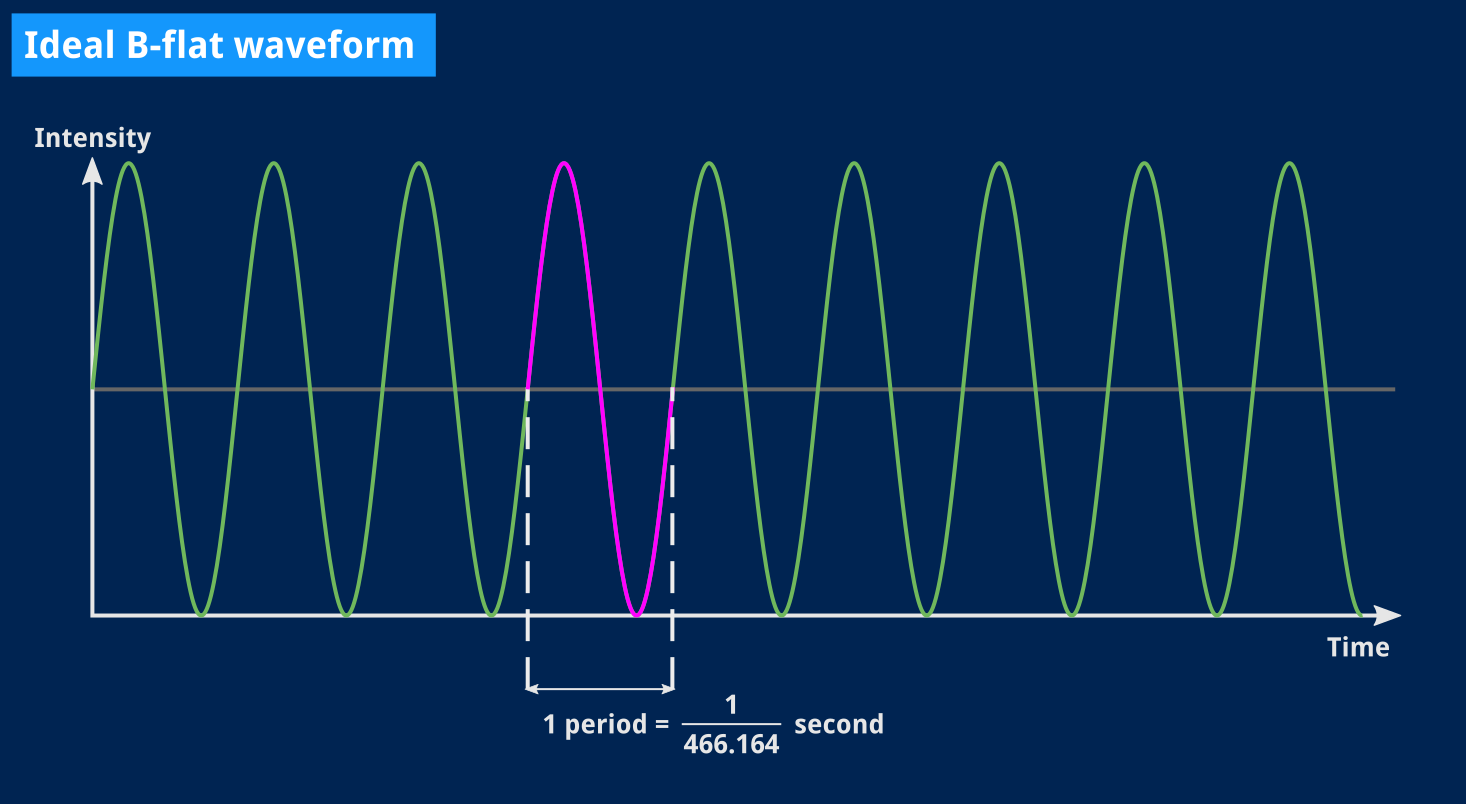
Does it have to be a sinusoid, though? If you checked the Wikipedia link above, you might have scrolled down and seen other shapes, or “waveforms” — triangular, sawtooth, square… And those are all valid sounds! So we can’t just somehow tell SDL to get cracking at 466 Hz. We have to define not only the frequency but also the shape of our waveform. And this is just for a single pure note. What if we want harmonics? Polyphony? Noise?

But wait, it gets worse!

Okay, so let’s say we only want to play a pure note for now. After all, the Game Boy only plays two short single notes when you boot it, right?

I’ve arbitrarily narrowed the problem down to two big questions I hope to answer in this article and the next ones:

• How does the Game Boy actually produce sound?
• How do we make SDL play that sound?

If you have watched the Ultimate Game Boy Talk you already know — or at least have a faint idea about — the former. I’ll admit it also gave me inklings about how I was going to tackle the issue. (Spoiler: more registers, more state machines, yay!)

However, having never really written any kind of sound-related code before, I thought I’d start with the latter. If only because until I started working on this, I truly had almost no idea how you made a computer play sound at a low level. I was very vaguely aware of what a sampling rate was, mostly from the old days of ripping CD tracks to WAV or encoding MP3s, but it still felt very abstract, so I first wanted to focus on writing code that just produced a pure note “by hand” using SDL².

Anyway, I rolled my sleeves up and started looking into sampling rates, pulse-code modulation, bit depth, quantization and various examples of code using SDL to play sounds, while trying to understand SDL’s audio API documentation at the same time.

It was tough, long and sometimes tedious, but as I waded through code snippets, questions on StackOverflow and so on, I felt I wasn’t alone.

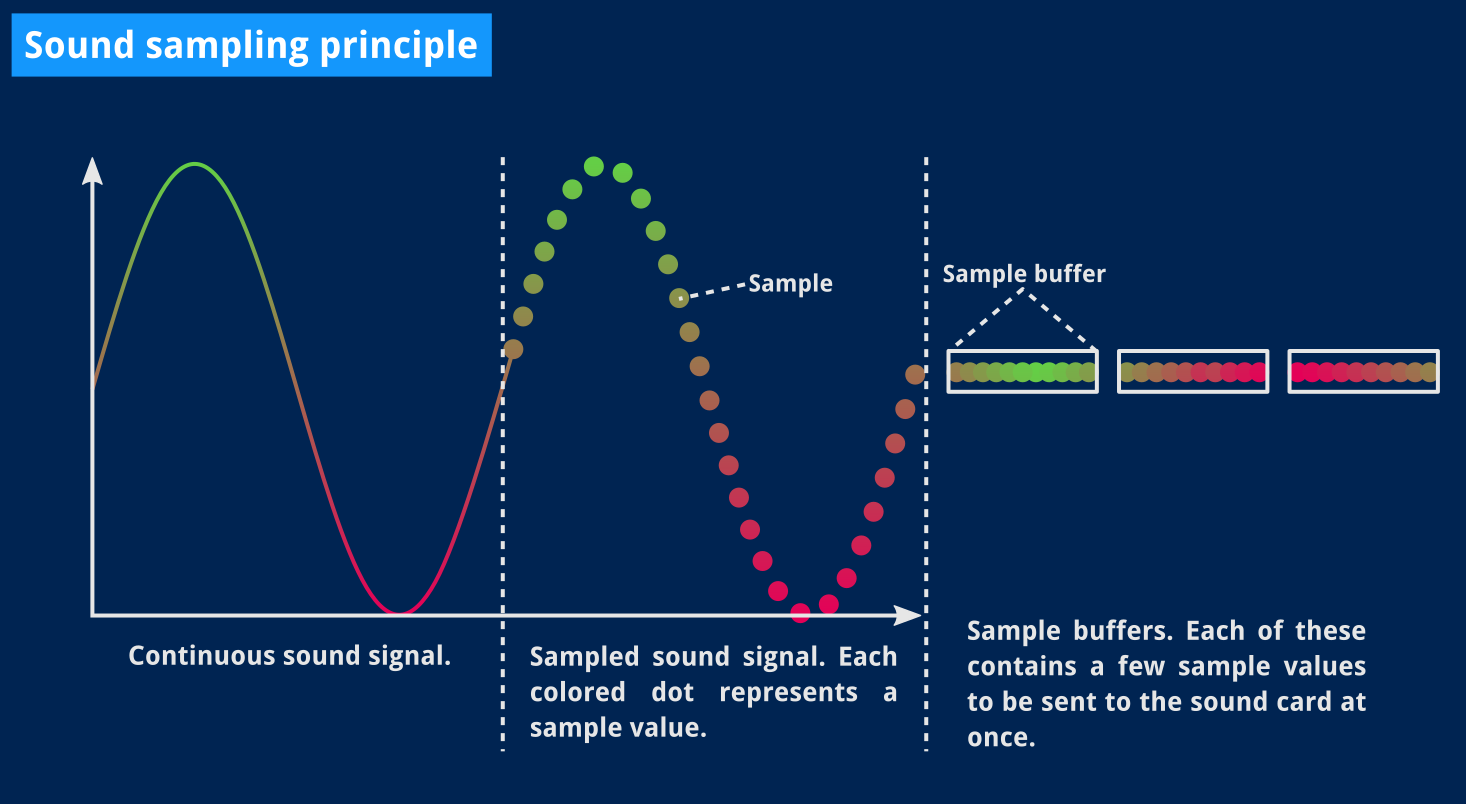
The theory itself is simple: no matter what our sound signal looks like, we just need to split it into a certain number of values (samples) per second (our sampling rate) and somehow feed that to the sound card.

Like we did with screen frames in the past, we’re going to have to slice our sound data into tiny time spans, and send a little bit of it to the sound card at a time. Just like we’re sending a new frame to the GPU at a theoretical 60 Hz… except we’ll have to do that a lot more often if we work even at a measly 22050 Hz sampling rate.

How do we even do that?

Just a bunch of numbers

It slowly dawned on me that sampling sound or sampling an image isn’t so different. To display a screen frame, we had to turn a bunch of colored dots into numbers, store those in a buffer and send that buffer to SDL. To play a sound, we’ll have to do something similar to a bunch of sound slices, store them in an audio buffer and send it to SDL.

And just as we didn’t magically happen to have a 160×144 bitmap image laying around in the Game Boy’s memory somewhere, we’ll need to make up the values defining those slices of sound as the Game Boy’s CPU ticks along. For now, we’ll just focus on how to come up with a bunch of numbers we could feed SDL to make it play a sound.

Let’s take a simpler note, like A, as its frequency, 440 Hz, is slightly easier to work with. To have SDL play that sound for one second, using a 22050 Hz sampling rate³, we have to feed it 22050 numbers, each representing the note’s approximate value for a 1/22050th of a second. Where do we get that value from? Well, from whatever amplitude the waveform is at that point in time, which entirely depends on the waveform’s shape now.

Here are examples using an artificially small sampling rate.

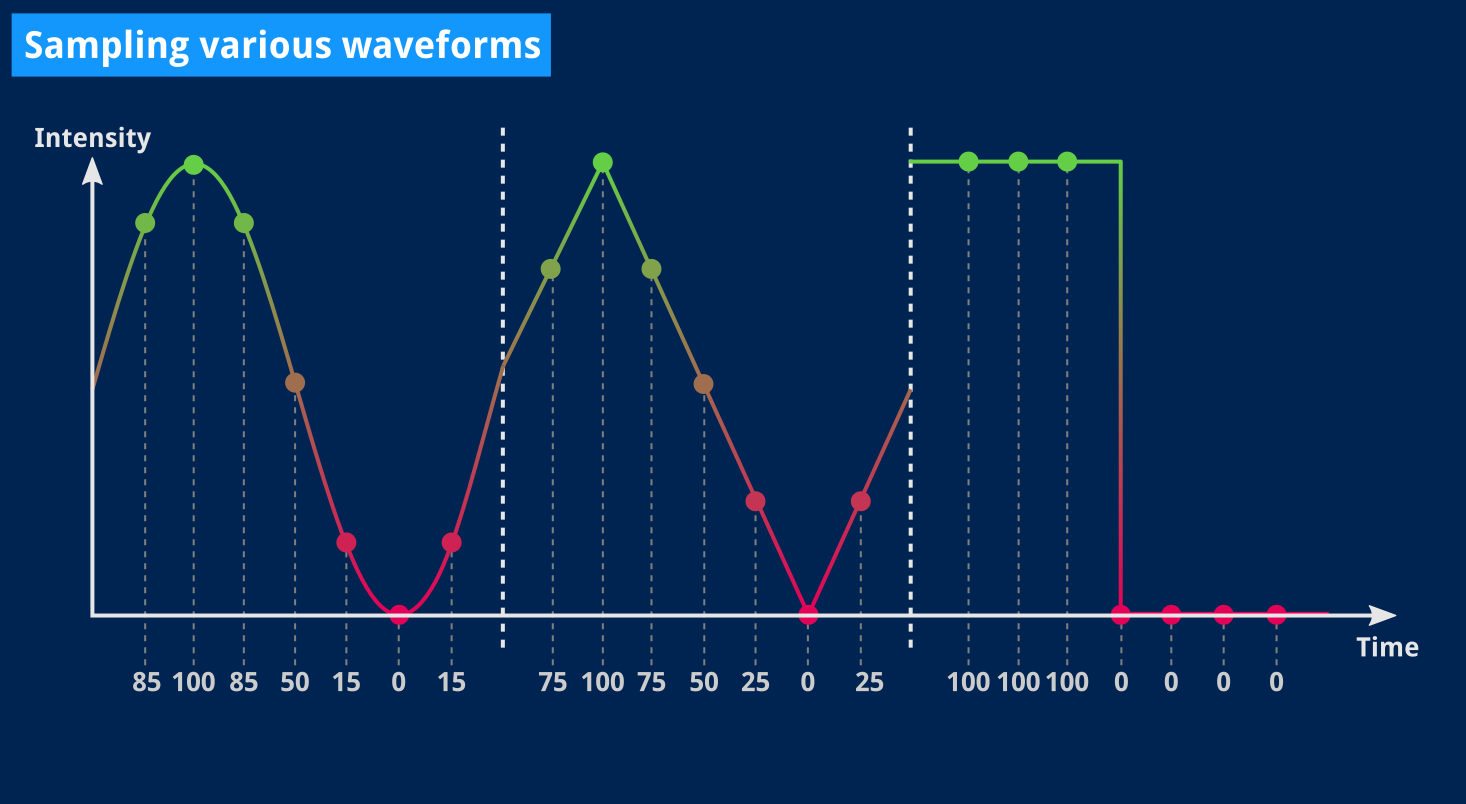
The simplest signal

From the picture above, it seems that using a square wave is going to require the least effort. Instead of having to precisely compute a given value at any given point in time, we’ll only have to keep track of when to turn it on or off. For now, that reduces the problem to finding out how many samples should be “on” and how many should be “off”. Then we can just repeat that pattern as many times as it takes to play one second of sound.

The math behind this isn’t complicated by any means but I suck at working with numbers that aren’t 0 or 1, so please bear with me as I reinvent the wheel and lay out a bunch of divisions below.

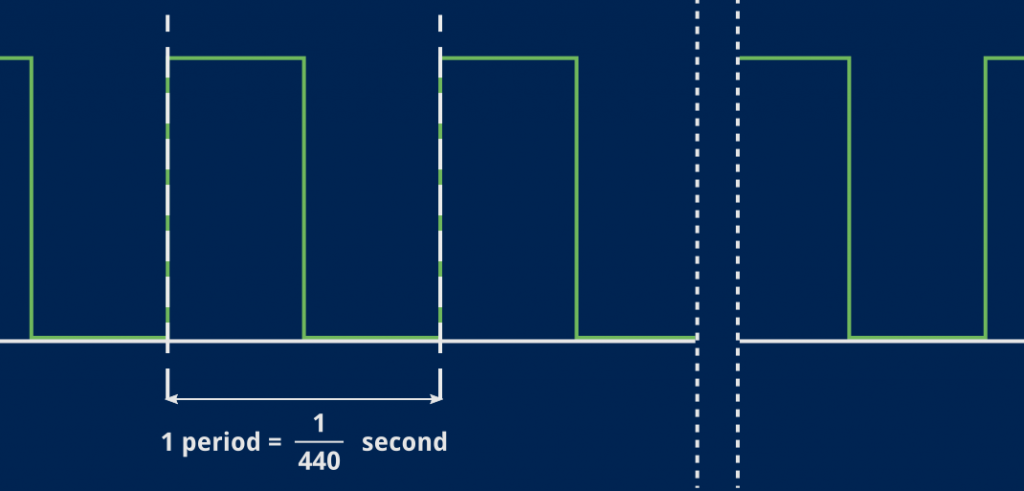
So! We want to generate a 440 Hz square signal. Which means that, for 1/440th of a second, our signal will go through one full period: for half of that 1/440th of a second, its value will be “on”, and for the other half, it will be “off”⁴.

I haven’t yet mentioned what numbers were going to represent “on” and “off”. We can actually use zero for “off”, and whatever constant value we pick for “on” will roughly represent the volume that note is played at. For the sake of today’s program, I’ll go with 127, which should be halfway between silence and full volume if we use unsigned 8-bit samples which can range from 0 to 255⁵.

What about timing?

But wait, if I wasn’t yet able to precisely time our 60 Hz display, how do I even send sound data to SDL 22050 times per second? The good news is that SDL itself will help us with that one.

The way SDL plays sound is by regularly calling a function we wrote and whose only job is to fill an audio buffer with sound samples⁶. How regularly this function is called should depend on our sampling rate and the size of the audio buffer, but it wasn’t obvious enough to me. So I tried timing it myself!

Hertz and ratios

Let’s talk numbers now. Here’s what we want our signal to look like:

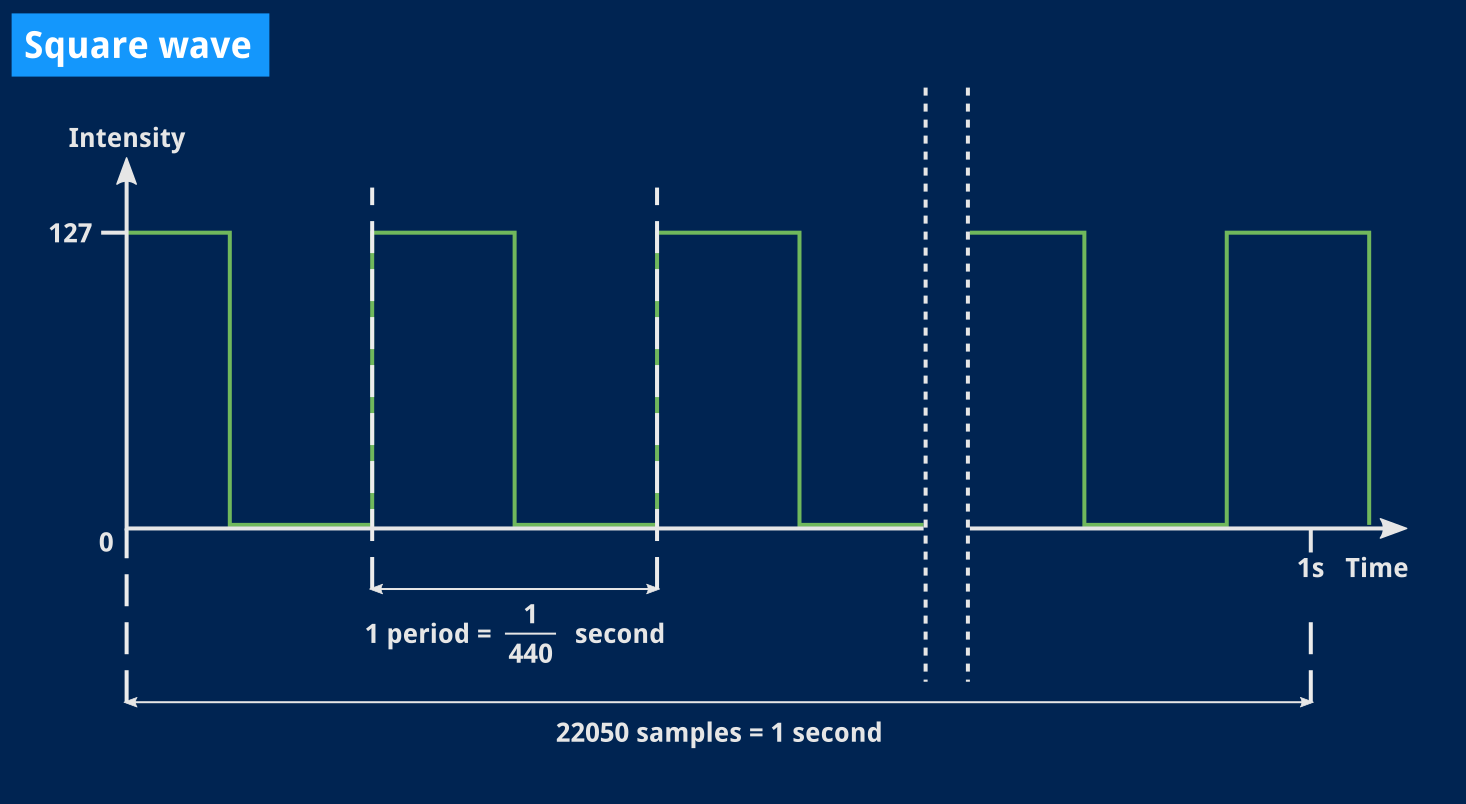
One period here is the time it takes for one full variation of our waveform. That time only depends on the note’s frequency. In our case, that A is 440 Hz so one full cycle will take 1/440 seconds.

Meanwhile, our sampling rate is 22050 Hz, which Wikipedia says is “used for lower-quality PCM and MPEG audio” and should be good enough for us to begin with. A single sample will cover 1/22050 seconds, but as mentioned earlier, we’ll always send a bunch of them at once to SDL, and how many we’ll send depends on the size of the audio buffer we’ll use. More about that in a moment.

Given the sampling rate and our note’s frequency, we can compute how many samples we’ll need to generate for a single period of that note:

Note frequency = 440 Hz
1 period = 1/440th of a second

Sampling rate = 22050 Hz
1 sample = 1/22050th of a second

How many samples in a single period of our note?
(1/440) / (1/22050) = (1/440) × 22050 = 22050 / 440 ≈ 50 samples

For our square signal, that amounts to 25 samples containing our maximum value, and 25 samples containing zero. Those 50 samples will then be repeated 440-ish times⁷ to make a one-second long sound.

Sizing the audio buffer

As we used a texture buffer to store pixels until it was time to display them, we need an audio buffer to exchange audio data with SDL. The texture buffer’s size was directly dictated by the screen’s dimensions. The audio buffer’s size, now, is actually up to us, and this lets us decide how often we’ll have to fill it.

Let’s take a common value I’ve seen several times in code I’ve looked at for inspiration: 1024 bytes. That’s a nice round number — SDL actually requires it to be a power of two. To save time now, I’ll also point out we’re working with stereo sound, which means we actually need to come up with two numbers for each 1/22050th of a second: one for the left channel, one for the right. It won’t be an issue here since we’ll be outputting exactly the same thing on the two channels, but that still means we need to size the audio buffer accordingly.

Moreover, the SDL function we’ll need to call to set up audio — which we’ll look at more closely in the next section — defines the audio buffer length as a number of sample frames. A sample frame is a bunch containing enough audio data samples for one single period of our sampling rate, that is, one for every channel. If we want independent sound values in stereo, we must yield two samples per 1/22050th of a second: one for each channel.

So the formula to compute our audio buffer size is:

Buffer size = 1024 bytes = 512 sample frames
                         = 2 × 512 8-bit samples (512 for each channel)

Why do we care about this subtlety? Well, we’ll use those numbers in a second to compute timings, and to this day I’m still not entirely sure not to be off by a factor of 2. Or 1/2. Or just 1/(number of channels). I don’t know, sound is complicated.

From buffer size to frequency

The next question I asked myself was: using the numbers above, how many buffers must we fill in a second?

Obviously, enough to reach the number of samples-per-second defined by our sampling rate. You see here that I’m using half of our buffer size because we actually want to send sound data for our two channels 22050 times a second.

So we need to fill 22050/512 ≈ 43 buffers to produce a second of sound. In other words, the buffer-filling function that SDL will regularly call should be invoked about 43 times per second (that’s roughly every 23 milliseconds, keep that number in mind, it will hopefully come up again).

If we want to adjust that, we can change the sampling rate or the buffer size. Halving the sampling rate would have us fill the audio buffer roughly every 45 ms, doubling it would make that every 12 ms and so on.

Now, let’s see if we can play that note!

Another simplistic program

Finding examples of playing raw samples in SDL using Go wasn’t easy so I pretty much entirely relied on SDL’s own example program shipping with the Go bindings that served as a base for what we’ll write today.

And after all I’ve written up to here, it turns out we’ll need surprisingly little in the way of code. Basically we just need to:

• Initialize SDL audio, which pretty much means giving SDL that sample rate and buffer size.
• Write a small function that SDL will call regularly to have it fill the audio buffer with “on” or “off” samples.

Initialization is done through SDL_OpenAudio⁸ by passing it audio parameters stored in an AudioSpec structure.

// Constant values you can tweak to see their effect on the produced sound.
const (
    tone            = 440   // "A" note at 440 Hz.
    sampleRate      = 22050 // How many sample frames to send per second.
    framesPerBuffer = 512   // Number of sample frames fitting the audio buffer.
    volume          = 127   // 50% volume for unsigned 8-bit samples.
    duration        = 3     // Desired duration of our note, in seconds.
)

func main() {
    // An AudioSpec structure containing our parameters. After calling
    // OpenAudio, it will also contain some values initialized by SDL itself,
    // such as the audio buffer size.
    spec := sdl.AudioSpec{
        Freq:     int32(sampleRate),
        Format:   sdl.AUDIO_U8,
        Channels: 2,
        Samples:  framesPerBuffer,
        Callback: sdl.AudioCallback(C.squareWaveCallback),
    }

    // We're asking SDL to honor our parameters exactly, or fail. You can ask
    // SDL to return what it can do if it can't handle your parameters, and
    // work with that instead.
    if err := sdl.OpenAudio(&spec, nil); err != nil {
        panic(err)
    }

    // We can check that SDL allocated an audio buffer that is exactly
    // (<number of samples per buffer> × <number of channels>) bytes long.
    fmt.Printf("Values obtained from OpenAudio:\n")
    fmt.Printf("Frequency: %d Hz\n", spec.Freq)
    fmt.Printf("Channels: %d\n", spec.Channels)
    fmt.Printf("Samples per buffer: %d\n", spec.Samples)
    fmt.Printf("Buffer size: %d bytes\n", spec.Size)

    // ... more coming soon.
}

On paper, there isn’t much to it: we store our bunch of numbers and a reference to our callback function⁹ in a structure and pass it straight to SDL. I also used unsigned 8-bit samples to keep things simple. I’ll call you back

Now to write the callback. It should be easy too: we store our square signal’s current amplitude (“on” or “off”) and update it every 25 samples¹⁰.

Unfortunately, exchanging raw audio data with SDL is something a little lower-level than filling a texture buffer. In the present case, it involves raw pointers, and that’s a whole thing I won’t get into that here because they’re completely irrelevant to sound itself and entirely specific to the programming language I happened to choose. That’s why the code excerpt below is glossing over a lot of internal shenanigans — that I still tried addressing in the actual source code.

// Work variables. I'm using global variables here because the program is so
// small. When we work with sound for real, we will store these in some
// structure whose address will be passed as user data each time our callback
// function is invoked.

var sampleFrames uint // Total count of sample frames sent to the sound card.
var duty uint         // Number of samples sent since last signal variation.

var isHigh = true // True for the "on" phase of our signal.
var quit bool     // Used by the callback to tell the main function to quit.

// Function filling an audio buffer with as many needed samples to represent a
// chunk of a square wave for the requested slice of time. We do this by keeping
// a running counter of generated samples, and toggle the sample value every 25
// samples.
//
// Function parameters have been simplified in this excerpt. An SDL audio
// callback normally must have a very precise signature.
func squareWaveCallback(buffer []uint8, bufLen int) {
    // We know we're working with 2 channels, so we have to duplicate our sample
    // value. Producing a different sound on each channel is left as an exercise
    // to the reader.
    for i := 0; i < bufLen; i += 2 {
        if isHigh {
            buffer[i] = volume
            buffer[i+1] = volume
        } else {
            buffer[i] = 0
            buffer[i+1] = 0
        }

        // Toggle the signal's volume between "on" and "off" when we have sent
        // as many samples as there are in one duty cycle. We are using a 50%
        // duty cycle here so this is (<sampling rate> / <note frequency>) / 2
        // or <sampling rate> / (2 × <note frequency>).
        if duty++; duty >= sampleRate/(tone*2) {
            isHigh = !isHigh // Toggle our signal "on" or "off".
            duty = 0
        }
    }

    // Count sample frames to know when the desired number of seconds has been
    // reached, then tell the main function we want to quit. Given our audio
    // buffer size, and the fact we're working with two channels, the number of
    // sample frames we just output is half the buffer size.
    sampleFrames += uint(bufLen / 2)
    if sampleFrames >= sampleRate*duration {
        quit = true
    }
}

If you don’t count all the comments I put in there, that’s less than 30 lines of code to output sound. Not bad, right? Then again, we’re only counting samples and adding either two zero or 0x7f samples in the audio buffer. We also keep a count of all the sample frames we sent to SDL to keep track of time: once we sent 22050 of them, one second should have passed.

And I can’t believe I spent so much time coming up with so little code. The thing that confused me most at first was the distinction between samples and sample frames. I’d use the former instead of the latter in my computations and end up with sound lasting half as long as wanted, or the opposite and it took twice as long and I wasn’t sure why… Have I mentioned that sound is hard?

But if we try it out, we will, indeed, hear a 3-second note — with potential crackling, which I thought was due to 22050 Hz not being a very high-quality sampling rate but was more likely due to using unsigned samples incorrectly.

This is not particularly impressive, but we still achieved two important things:

• We played a sound, using only five numbers.
• We played a sound for a pretty specific duration.

Timing is key

It’s that duration I want to focus on. If I time the program in my terminal, I see it takes a tiny bit more than 3 seconds to run, but that’s not a very good way to measure it because the code itself does a little more than just playing sound. Now, if I open the small video shown above in a sound editor, we can see that the sound we produced lasted almost exactly 3 seconds — and you can see the signal’s amplitude when it’s “on” is about exactly 50%.

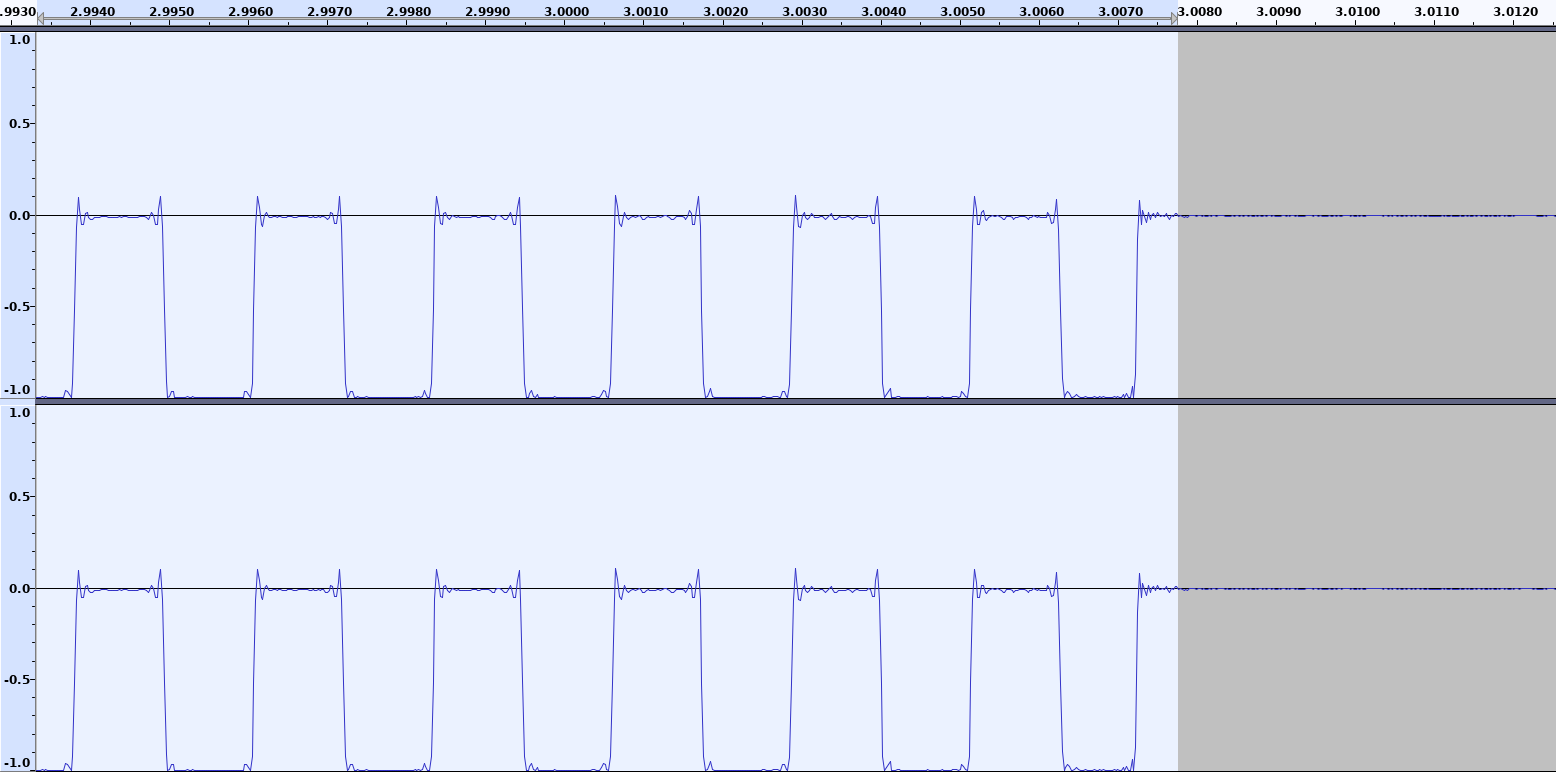
So, hey, it does look like our audio driver could be used as a timing source. We managed to play sound with timings accurate to (roughly) one 22050th of a second. And now I have even more questions that will need at least one more article to answer. Most importantly: how can we use that newfound timing source with our emulator?

The Game Boy’s clock runs at 4 194 304 Hz which is comparatively fast (1 tick every 0.2 µs or almost every microsecond for a 4-clock CPU cycle). But that means we could use only a fraction of the time spent executing our Tick() methods to fill audio buffers, maybe stop when they’re full, and flush them when the callback is invoked. If we didn’t fill them fast enough (i.e. the callback is invoked too soon before the emulator could execute enough ticks) we should hear sound tearing, but that would still be a start.

How do we check how often that callback is actually invoked anyway?

SDL can help us again here. It’s got a function to tell us how many milliseconds have elapsed since the program was started. Using our brand new square wave generator, I recorded the current milliseconds count every time the callback function was invoked.

// List of timestamps (in milliseconds elapsed since the beginning of the
// program's execution) at each invocation of our callback function. We'll use
// these to compute how often the callback was invoked in the end.
var ticksInCallback []int

// Abridged callback.
func squareWaveCallback(buf []uint8, bufLen int) {
    // ... rest of the callback above ...

    // Store current ticks count. We'll analyze all of them later.
    ticksInCallback = append(ticksInCallback, int(sdl.GetTicks()))
}

I could then check the interval between each two consecutive callback invocations just before the program ends, at the end of our main() function. Since, the first time I tried that, I ended up with quite a few different (though close) values, I also wanted to check what the average was.

    // ... rest of main() function above ...

    // Just to get a feel for it, print all recorded timestamp values. They
    // should be incremental and close to one another.
    fmt.Printf("Tick values at each callback invocation:\n")
    fmt.Println(ticksInCallback)

    // Now turn that list of increasing timestamps into a list of intervals
    // between each two consecutive values. This should yield a list of
    // numbers that are much closer in value.
    var intervals []int
    for i := 0; i < len(ticksInCallback)-1; i++ {
        intervals = append(intervals, ticksInCallback[i+1]-ticksInCallback[i])
    }
    fmt.Printf("Intervals between consecutive callback invocations:\n")
    fmt.Println(intervals)

    // And finally compute the average value for those intervals (I've only
    // computed the arithmetic mean, further analysis is left as an exercise to
    // the reader.)
    average := 0
    for _, interval := range intervals {
        average += interval
    }

    average /= len(intervals)

    fmt.Printf("Average interval: %dms\n", average)

And by running the program again, we can now have a look at those numbers.

…/06-sound-is-complicated/code $ go run ./sound-is-complicated.go
Values obtained from OpenAudio:
Frequency: 22050 Hz
Channels: 2
Samples per buffer: 512
Buffer size: 1024 bytes

The callback was invoked 130 times:
[21 44 67 90 113 136 159 182 206 229 252 275 298 322 353 376 399 422 445 468 491 514 538
561 584 607 630 653 676 699 722 745 768 791 814 837 860 883 906 929 952 976 999 1021 1044
1067 1090 1113 1136 1159 1181 1204 1227 1250 1274 1297 1320 1344 1374 1397 1420 1444 1467
1490 1513 1536 1559 1582 1605 1628 1651 1674 1697 1720 1743 1766 1789 1812 1835 1858 1881
1904 1927 1950 1973 1996 2018 2041 2064 2087 2110 2133 2156 2179 2202 2225 2256 2279 2301
2325 2349 2372 2395 2418 2441 2464 2487 2510 2533 2556 2578 2601 2624 2647 2670 2693 2716
2739 2762 2785 2808 2831 2854 2877 2900 2924 2947 2970 2993 3015]

Intervals between consecutive callback invocations:
[23 23 23 23 23 23 23 24 23 23 23 23 24 31 23 23 23 23 23 23 23 24 23 23 23 23 23 23 23 23
23 23 23 23 23 23 23 23 23 23 24 23 22 23 23 23 23 23 23 22 23 23 23 24 23 23 24 30 23 23
24 23 23 23 23 23 23 23 23 23 23 23 23 23 23 23 23 23 23 23 23 23 23 23 23 22 23 23 23 23
23 23 23 23 23 31 23 22 24 24 23 23 23 23 23 23 23 23 23 22 23 23 23 23 23 23 23 23 23 23
23 23 23 23 24 23 23 23 22]

Average interval: 23ms

Lots of hand-waving aside, we can see right away that we filled the audio buffer 130 times. That’s pretty much three times 43, which was the number of buffers we figured out should be filled in a second. Whew!

The shortest time recorded by SDL between two calls was 22ms, longest was 31ms. But the mean time across the 130 invocations was just about… 23ms, hooray!

What’s next?

I get the feeling all of this should have been obvious from the very beginning, but it wasn’t to me. For some reason I had to confirm it through experiment and now I feel comfortable enough with sound in SDL to start thinking about using it in our emulator.

Today we’ve seen how to slice a sound into samples to play it via SDL for a given duration, with a surprising degree of accuracy. We still need to make that happen in the emulator, which only raises further questions:

• How do we generate sound samples from within the emulator?
• How do we fit our emulator’s main loop and the SDL audio callback together to have better timings?

In the next article, I’ll tackle the first issue. Part of today’s problem was to transform some arbitrary sound into some waveform and then some numbers. We’ll see how the Game Boy itself does it and how to use similar numbers (sampling rate, tone frequency, duty cycle…) in our code.

Then, we’ll try and make all of that happen within some audio callback. Until now, while writing these articles, I always had pre-existing working code taken from my emulator in some shape or form to back me up. At the time of this writing, this is no longer the case and I’m excited to be working on new features again, frustrating as they may be.

So, again, I’m sorry if it’s all a little tedious. But we’re still a small step closer to achieving full boot ROM execution!

Thank you for reading.

References

• The SDL audio API documentation
• The SDL example code in Go bindings
• Wikipedia:
  • A (musical note)
  • Audio bit depth
  • Pulse-code modulation
  • Quantization
  • Sampling (signal processing)
  • Sine wave
• Play a sound with SDL2 (no SDL_Mixer)
• Example program: sound is complicated

You can download the example program above and run it anywhere from the command line:

$ go run sound-is-complicated.go